Numerics Library for Unity

Library version: 1.0.0

BigParrot Numerics Library for Unity is a tool that can increase productivity in numerical computing tasks in Unity and C#.

It provides more than 100 methods, including easily and flexible array manipulation routines, useful mathematical functions, linear algebra and polynomial routines, Fast Fourier transforms, and signal processing.

It can be used directly in Unity without requiring additional installation or environment setup, and it is compatible with mobile platforms as well.

E-mail: bigparrotstudio@gmail.com (Feature requests, bug reports or contact)

Getting Started
NumericsArray
Array Manipulation
Mathmatical Functions
Statistics
Linear Algebra
Polynomial
Signal Processing

Getting Started

Install package to your project by using the Package Manager window.

Importing an Asset Store package

It targets .NET Standard 2.1 or higher and Unity 2021 LTS or higher.

https://docs.unity3d.com/Manual/dotnetProfileSupport.html

In the .NET Standard 2.0 environment, change the API compatibility to .NET 4.x.

https://learn.microsoft.com/en-us/visualstudio/gamedev/unity/unity-scripting-upgrade

using BigParrot.Numerics;
using BigParrot.Numerics.SignalProcessing;

NumericsArray

The NumericsArray serves as the primary storage space, providing arrays of various types that inherit from NumericsArray<T>.

Array	Data Type
DoubleArray	double
FloatArray	float
IntArray	int
BoolArray	bool
ComplexArray	BigParrot.Numerics.Complex

Each array class will have an array based on its data type. Therefore, the supported features or behaviors may vary for each type.

Array declaration

To declare an NumericsArray, you can create a class of the desired type.

Here is an example that creates an array of type double with length 5 and an array of type boolean with length 3:

DoubleArray a = new DoubleArray(5);
BoolArray b = new BoolArray(3);

> Output:
[0, 0, 0, 0, 0]
[false, false, false]

To declare an 2-dimensional array, you would input the row and column sizes.

The following creates an array of type int with 2 rows and 5 columns:

IntArray a = new IntArray(2, 5);

> Output:
[[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]]

You can use the Empty method to create an empty array. The following creates an empty array of type float:

FloatArray a = FloatArray.Empty;

> Output:
[]

You can also create an array by providing an existing C# array as an argument:

IntArray a = new IntArray(new int[] { 1, 2, 3, 4, 5, 6 });
IntArray b = new IntArray(new int[,] { { 1, 2, 3 }, { 4, 5, 6 } });

Array properties

The properties that contain information about the shape and size of an array are as follows:

Properties	Description
NDim	Returns the number of dimensions of the array.
Length	Returns the total number of elements in the array.
RowCount	Returns the number of rows in the array.
ColumnCount	Returns the number of columns in the array.
Shape	Returns an `ArrayShape` structure containing the above elements.

In a one-dimensional array, RowCount is 0, and Length and ColumnCount are equal.

In a two-dimensional array, Length is equal to the product of RowCount and ColumnCount.

IntArray a = new IntArray(3, 5);
int ndim = a.NDim;
int length = a.Length;
int rowCount = a.RowCount;
int columnCount = a.ColumnCount;

> Output:
NDim: 2
Length: 15
RowCount: 3
ColumnCount: 5

Currently, arrays with a maximum of 2 dimensions are supported. We plan to support higher-dimensional arrays in the future.

Indexing and slicing

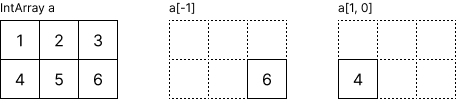
Like C# arrays, NumericsArray's indexing is zero-based, but it also supports negative indexing. For instance, -1 accesses the last element of the array.

IntArray a = new IntArray(new int[] { 1, 2, 3, 4, 5 });
int b = a[-1];

> Output:
5

For 2-dimensional array, both 2-dimensional indexing and 1-dimensional indexing are possible. In this case, the index order follows row-major order.

IntArray a = new IntArray(new int[,] { { 1, 2, 3 }, { 4, 5, 6 } });
int b = a[1, 0];
int c = a[3];

> Output:
4
4

In addition to accessing it through the array indexer, you can also slice a specific range of array elements using the Get or Slice functions.

The following is an example of using the Get function to slice elements from rows 0 to 2 and columns 1 to 2 in an array.

IntArray a = new IntArray(new int[,] { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } });
IntArray b = a.Get(new Range(0, 2), new Range(1, 2));

> Output:
[[2, 3],
[5, 6]]

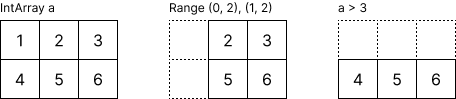
You can also index an array using conditions. Here's an example that indexes elements greater than 3:

IntArray a = new IntArray(new int[,] { { 1, 2, 3 }, { 4, 5, 6 } });
IntArray b = a.Get(a > 3);

> Output:
[4, 5, 6]

Operators

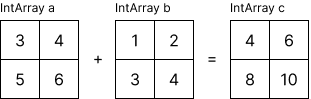
You can easily perform operations between arrays and scalars or between arrays. Arithmetic operators provided include +, -, *, /, and %.

IntArray a = new IntArray(new int[,] { { 3, 4 }, { 5, 6 } });
IntArray b = new IntArray(new int[,] { { 1, 2 }, { 3, 4 } });
IntArray c = a + b;

> Output:
[[4, 6],
[8, 10]];

In C#, the % operator behaves as the remainder operator, which is different from Python's % operator. To achieve the same result as Python's % operator in C#, you should use the Modulo method.

Comparison operators provided include ==, !=, >, >=, <, <=, &, |, ^.

When you compare elements of two arrays using these operators, the result is returned as a BoolArray.

IntArray a = new IntArray(new int[] { 5, 2, 3 });
IntArray b = new IntArray(new int[] { 4, 2, 6 });
BoolArray r = a > b;

> Output:
[true, false, false]

If you want to determine whether two arrays have exactly the same shape and elements, you can use the ArrayEquiv. Equals compares whether two arrays are the same object.

Broadcasting

To perform operations between two arrays, their shapes and sizes must match, or one of the arrays' axis sizes must be 1.

For example, if you want to perform addition operation between two 1-dimensional arrays. Assuming that the length of array b is 1, you can perform the operation by assuming that it matches the size of array a. Therefore, each element of a performs addition with the first index of b.

IntArray a = new IntArray(new int[] { 3, 4, 5 });
IntArray b = new IntArray(new int[] { 1 });
IntArray c = a + b;

> Output:
[4, 5, 6];

However, if the length of b is 2, an error will occur.

The same applies to 2-dimensional arrays. In the case of the following two arrays, there is no problem performing operations because the row size of array b is 1. If the row size is 1 or the column size is 1, it can extend it to perform calculations.

IntArray a = new IntArray(new int[,] { { 3, 4 }, { 5, 6 } });
IntArray b = new IntArray(new int[,] { { 1, 2 } });
IntArray c = a + b;

> Output:
[[4, 6],
[6, 8]]

Array type conversion

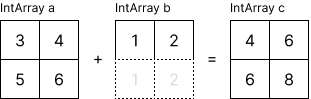
To convert the type of an array, type conversion functions such as ToIntArray and ToDoubleArray are provided.

Here's an example of converting a DoubleArray to an IntArray using the provided type conversion functions:

DoubleArray a = new DoubleArray(new double[] { 1.1, 2.2, 3.3 });
IntArray b = a.ToIntArray();

> Output:
[1, 2, 3]

When performing type conversion, it use the Convert class in C#. For detailed information, please refer to the documentation of that class.

https://learn.microsoft.com/en-us/dotnet/api/system.convert?view=netframework-4.8.1

Array creation functions

When creating arrays, various methods are provided to generate arrays with a specified interval or shapes.

Arange function generates an array with evenly spaced values within a given interval.

DoubleArray a = DoubleArray.Arange(5, 25, 3);

> Output:
[5, 8, 11, 14, 17, 20, 23]

Linspace function generates an array with evenly spaced numbers over a specified interval.

The following example creates an array with a length of 5, evenly spaced between 2 and 10:

DoubleArray a = DoubleArray.Linspace(2, 10, 5);

> Output:
[2, 4, 6, 8, 10]

Logspace function generates an array with logarithmically spaced numbers over a specified interval.

Eye function creates a identity matrix. Here's an example to create a 3-by-3 identity matrix:

DoubleArray a = DoubleArray.Eye(3);

> Output:
[[1, 0, 0],
[0, 1, 0]]
[0, 0, 1]]

Diagonal function creates a diagonal array or extract a diagonal.

DoubleArray d = new DoubleArray(new double[] { 1, 2, 3 });
DoubleArray a = DoubleArray.Diagonal(d);

> Output:
[[1, 0, 0],
[0, 2, 0],
[0, 0, 3]]

DoubleArray d = new DoubleArray(new double[,] { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } });
DoubleArray a = DoubleArray.Diagonal(d);

> Output:
[1, 5, 9]

Triu function returns the upper triangular portion of array.

Vander function creates a Vandermonde matrix.

Random Sampling

Random function creates an array filled with random values within the given range. Here's an example of creating a 2-dimensional array of size 3-by-3 using the ArrayShape class and filling it with random values between 0 and 10:

IntArray a = IntArray.Random(new ArrayShape(3, 3), 0, 10);

> Output:
[[6, 2, 7],
[4, 3, 9],
[1, 5, 4]]

RandomChoice function generates a random samples from a given 1-dimensional array. Here's an example of creating a 1-dimensional array of size 5 and filling it with randomly chosen elements from array r:

IntArray a = new IntArray(new int[] { 2, 4, 5, 8 });
IntArray b = IntArray.RandomChoice(a, new ArrayShape(5));

> Output:
[4, 2, 8, 4, 5]

RandomNormal function generates a random samples from a normal distribution.

DoubleArray a = DoubleArray.RandomNormal(new ArrayShape(100));

> Output:
[0.3207178493394863, 1.8498536815260844, -0.9893994057738318, ... ]

Array Manipulation

Axis of the array

When manipulating arrays, you can determine which axis to access elements along.

Axis.None: access starts from the zero index in the order of indices.
Axis.Row: accesses along the rows.
Axis.Column: accesses along the columns.

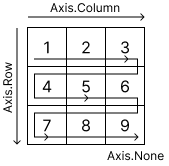
In a one-dimensional array, the axis is always Axis.None, and changing it to another axis has no effect. When Axis.None is used in a two-dimensional array, it accesses it as if it were a one-dimensional array.

Change array elements

Set function sets the value of the elements at the specified position. Here is an example of changing a element at row index 1 and column index 1:

IntArray a = new IntArray(new int[,] { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } });
IntArray b = new IntArray(new int[] { 10, 11 });
a.Set(b, 1, 1);

> Output:
[[1, 2, 3],
[4, 10, 11],
[7, 8, 9]]

Using functions like SetRow or SetColumn, you can replace specific columns or rows with different elements.

IntArray a = new IntArray(new int[,] { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } });
IntArray b = new IntArray(new int[] { 10, 11, 12 });
a.SetColumn(b, 0);

> Output:
[[10, 2, 3],
[11, 5, 6],
[12, 8, 9]]

Fill function fills the array with a given values. If an array is provided as an argument, its contents will be used to fill all elements.

IntArray a = new IntArray(new int[] { 1, 2, 3, 4 });
IntArray b = new IntArray(new int[] { 5, 6 });
a.Fill(b);

> Output:
[5, 6, 5, 6]

Swap function swaps elements at specified positions in an array. In the following example, the first and last rows (-1) are swapped.

IntArray a = new IntArray(new int[,] {{ 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 }});
a.Swap(0, -1, Axis.Row);

> Output:
[[7, 8, 9],
[4, 5, 6],
[1, 2, 3]]

Roll function shifts the elements of the array. If the shift argument is positive, the elements are shifted in the positive direction; if negative, the elements are shifted in the negative direction.

IntArray a = new IntArray(new int[] { 1, 2, 3, 4, 5 });
IntArray b = IntArray.Roll(a, 2);

> Output:
[4, 5, 1, 2, 3]

Place function changes elements that meet the condition with the given array elements. The following is an example of changing an element with value 1 to a given array.

IntArray a = new IntArray(new int[] { 1, 1, 1, 2, 2, 2 });
IntArray vals = new IntArray(new int[] { 5, 6, 7 });
IntArray b = IntArray.Place(a, a == 1, vals);

> Output:
[5, 6, 7, 2, 2, 2]

Shuffle function shuffles all elements of an array randomly.

Clip function limits the elements of an array so that they do not fall below minValue or exceed maxValue.

Repeat function returns an array with each element of the original array repeated. If a 2-dimensional array is repeated, it will be repeated along the specified axis.

Add array elements

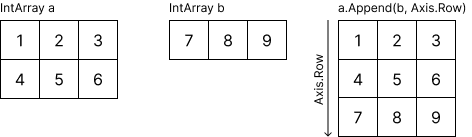
Append function adds new elements to the end of the array.

IntArray a = new IntArray(new int[] { 1, 2, 3, 4, 5 });
IntArray b = new IntArray(new int[] { 6, 7 });
a.Append(b);

> Output:
[1, 2, 3, 4, 5, 6, 7]

You can add a new row or a new column based on the specified axis. Here's an example of adding a new row to a 2-dimensional array:

IntArray a = new IntArray(new int[,] { { 1, 2, 3 }, { 4, 5, 6 } });
IntArray b = new IntArray(new int[,] { { 7, 8, 9 } });
a.Append(b, Axis.Row);

> Output:
[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]

Insert function inserts new elements into the array at the specified index.

IntArray a = new IntArray(new int[] { 1, 2, 4, 5 });
a.Insert(2, 3);

> Output:
[1, 2, 3, 4, 5]

Concatenate function concatenates two or three arrays. Here's an example of concatenating three 1-dimensional arrays:

IntArray a = new IntArray(new int[] { 1, 2, 3 });
IntArray b = new IntArray(new int[] { 4, 5 });
IntArray c = new IntArray(new int[] { 6, 7, 8 });
IntArray d = IntArray.Concatenate(a, b, c);

> Output:
[1, 2, 3, 4, 5, 6, 7, 8]

Remove array elements

Remove function removes a specific region of the array. Below is an example of removing elements from the last row (-1) of a 2-dimensional array:

IntArray a = new IntArray(new int[,] { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } });
IntArray b = IntArray.Remove(a, -1, Axis.Row);

> Output:
[[1, 2, 3],
[4, 5, 6]]

The Trim function trims the leading and trailing zeros from an array.

Change array size or shape

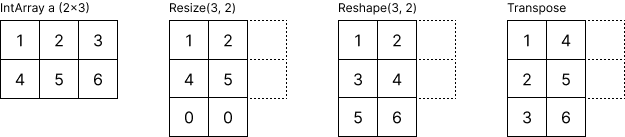
Resize function changes the size of the array. If the new size is smaller, existing elements will be removed. It is also allowed to change the dimensions of the array. Here's how you can use it:

IntArray a = new IntArray(new int[,] { { 1, 2, 3 }, { 4, 5, 6 } });
a.Resize(3, 2);

> Output:
[[1, 2],
[4, 5],
[0, 0]]

Reshape function changes the shape of a 2-dimensional array without altering its total size. When providing newRowCount and newColumnCount, the total size must be preserved. If one of the arguments is set to -1, it will be automatically determined to maintain the total size.

Here's an example of reshaping a 2-by-3 array into a 3-by-2 array:

IntArray a = new IntArray(new int[,] { { 1, 2, 3 }, { 4, 5, 6 } });
IntArray b = IntArray.Reshape(a, 3, 2);

> Output:
[[1, 2],
[3, 4],
[5, 6]]

Transpose function transposes the array.

IntArray a = new IntArray(new int[,] { { 1, 2, 3 }, { 4, 5, 6 } });
IntArray b = IntArray.Transpose(a);

> Output:
[[1, 4],
[2, 5]
[3, 6]]

Ravel function flattens a 2-dimensional array into a 1-dimensional array. If isRowMajor is set to false, it flattens the array in column-major order. Here's how you can use it:

IntArray a = new IntArray(new int[,] { { 1, 2, 3 }, { 4, 5, 6 } });
IntArray b = IntArray.Ravel(a);
IntArray c = IntArray.Ravel(a, false);

> Output:
[1, 2, 3, 4, 5, 6]
[1, 4, 2, 5, 3, 6]

Reverse function reverses the order of elements. Here's an example of reversing the array along the row axis in a 2-dimensional array:

IntArray a = new IntArray(new int[,] { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } });
IntArray b = IntArray.Reverse(a, Axis.Row);

> Output:
[[7, 8, 9],
[4, 5, 6]
[1, 2, 3]]

Sorting and seraching routines

Sort function sorts the array. Arrays are sorted in ascending order.

For a 1-dimensional array, all elements are sorted. For a 2-dimensional array, elements are sorted along each axis. If the axis is None, the entire array is sorted in row-major order.

Here's an example of sorting each row along the column axis in a 2-dimensional array:

IntArray a = new IntArray(new int[,] { { 2, 3, 1 }, { 5, 4, 6 }, { 9, 8, 7 } });
IntArray b = IntArray.Sort(a, Axis.Column);

> Output:
[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]

ArgSort function returns the indices of the sorted array as an IntArray. Here's how you can use it:

DoubleArray a = new DoubleArray(new double[] { 3.5, 1.5, 4.5, 2.5 });
IntArray b = DoubleArray.ArgSort(a);

> Output:
[1, 3, 0, 2]

Unique function returns the unique elements of an array as a 1-dimensional array.

IntArray a = new IntArray(new int[] { 1, 2, 2, 3, 4, 4 });
IntArray b = IntArray.Unique(a);

> Output:
[1, 2, 3, 4]

Extract function returns elements that satisfy the specified condition as a 1-dimensional array. Here's an example of extracting elements from array a that are greater than 2 and less than or equal to 4:

IntArray a = new IntArray(new int[] { 1, 2, 3, 3, 4, 4, 5 });
IntArray b = IntArray.Extract(a > 2 & a <= 4, a);

> Output:
[3, 3, 4, 4]

Take function returns elements corresponding to the specified indices as a new array. Here's how you can use it:

DoubleArray a = new DoubleArray(new double[] { 1.5, 2.5, 3.5, 4.5, 5.5 });
IntArray indices = new IntArray(new int[] { 2, 4, 3 });
DoubleArray b = DoubleArray.Take(a, indices);

> Output:
[3.5, 5.5, 4.5]

NonZero function return the indices of the elements that are non-zero.

Mathmatical Functions

Arithmetic Operations

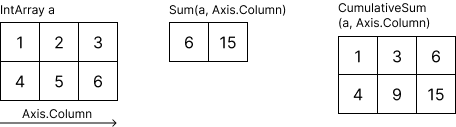
Sum function returns the sum of elements in the array.

IntArray a = new IntArray(new int[] { 1, 2, 3 });
int sum = a.Sum();

> Output:
6

You can calculate the sum along each axis. Here's an example of calculating the sum of each row along the column axis:

IntArray a = new IntArray(new int[,] { { 1, 2, 3 }, { 4, 5, 6 } });
IntArray sum = IntArray.Sum(a, Axis.Column);

> Output:
[6, 15]

CumulativeSum function returns the cumulative sum of elements in the array. In a 2-dimensional array, you can calculate the cumulative sum along each axis.

IntArray a = new IntArray(new int[] { 1, 2, 3 });
IntArray sum = IntArray.CumulativeSum(a);

> Output:
[1, 3, 6]

Product function returns the product of elements in the array.

IntArray a = new IntArray(new int[] { 2, 3, 4 });
int prod = a.Product();

> Output:
24

CumulativeProduct function returns the cumulative product of elements in the array.

IntArray a = new IntArray(new int[] { 2, 3, 4 });
IntArray prod = IntArray.CumulativeProduct(a);

> Output:
[2, 6, 24]

Difference function calculates the discrete difference of elements in the array. The first difference is given by as a[1] - a[0]. Here's an example of computing differences in a one-dimensional array:

IntArray a = new IntArray(new int[] { 1, 3, 7, 12 });
IntArray d = IntArray.Difference(a);

> Output:
[2, 4, 5]

Exponents and Logarithms

Exp function calculates the exponential of each element in the array.

DoubleArray a = new DoubleArray(new double[] { 1, 2, 3 });
DoubleArray b = DoubleArray.Exp(a);

> Output:
[2.718281828459045, 7.38905609893065, 20.085536923187668]

Sqrt function calculates the square root of each element in the array.

DoubleArray a = new DoubleArray(new double[] { 2, 3, 4 });
DoubleArray b = DoubleArray.Sqrt(a);

> Output:
[1.4142135623730951, 1.7320508075688772, 2]

Log function calculates the natural logarithm of each element in the array.

DoubleArray a = new DoubleArray(new double[] { 2, 3, 4 });
DoubleArray b = DoubleArray.Log(a);

> Output:
[0.6931471805599453, 1.0986122886681098, 1.3862943611198906]

Log10 function calculates the base 10 logarithm of each element in the array.

Trigonometry

Sin, Cos, Tan, etc. compute trigonometric functions element-wise.

DoubleArray a = new DoubleArray(new double[] { 2, 3, 4 });
DoubleArray b = DoubleArray.Sin(a);

> Output:
[0.9092974268256817, 0.1411200080598672, -0.7568024953079282]

Hypotenuse function returns the hypotenuse of a right-angled triangle.

DoubleArray a = new DoubleArray(new double[] { 2, 3, 4 });
DoubleArray b = new DoubleArray(new double[] { 5, 6, 7 });
DoubleArray h = DoubleArray.Hypotenuse(a, b);

> Output:
[5.385164807134504, 6.708203932499369, 8.06225774829855]

Rad2Deg and Deg2Rad functions convert elements of an array from radians to degrees or from degrees to radians, respectively.

DoubleArray a = new DoubleArray(new double[] { 45, 90, 180 });
DoubleArray b = DoubleArray.Deg2Rad(a);

> Output:
[0.7853981633974483, 1.5707963267948966, 3.141592653589793]

Complex Numbers

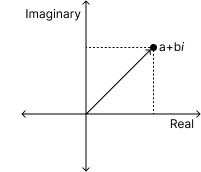
You can create a ComplexArray composed of the BigParrot.Numerics.Complex struct to perform complex number calculations.

ComplexArray a = new ComplexArray(new Complex[] { new Complex(1, 2), new Complex(-2, 0) });

> Output:
[1+2j, -2+0j]

The Real function returns only the real part of the complex array, while the Imag function returns only the imaginary part of the complex array.

ComplexArray a = new ComplexArray(new Complex[] { new Complex(1, 2), new Complex(-2, 0) });
DoubleArray real = a.Real();
DoubleArray imag = a.Imag();

> Output:
[1, -2]
[2, 0]

Conjugate function returns the complex conjugate of the complex array.

ComplexArray a = new ComplexArray(new Complex[] { new Complex(1, 2), new Complex(-2, 1) });
ComplexArray b = ComplexArray.Conjugate(a);

> Output:
[1-2j, -2-1j]

Angle function returns the angle of the complex number elements. The returned angle is in radians, but if the isDegrees parameter is set to true, it returns the angle in degrees.

ComplexArray a = new ComplexArray(new Complex[] { new Complex(0, 1), new Complex(1, 0), new Complex(1, 1) });
DoubleArray b = ComplexArray.Angle(a, true);

> Output:
[90, 0, 45]

Miscellaneous Functions

Abs function returns the absolute values of the elements.

ComplexArray a = new ComplexArray(new Complex[] { new Complex(0, 1), new Complex(1, 2) });
DoubleArray b = ComplexArray.Abs(a);

> Output:
[1, 2.2360679774997]

Power function returns the elements raised to the power.

IntArray a = new IntArray(new int[] { 2, 3, 4 });
IntArray b = IntArray.Power(a, 3);

> Output:
[8, 27, 64]

Round function rounds the elements to the given number of decimal.

DoubleArray a = new DoubleArray(new double[] { 1.2, 1.5, 1.8 });
DoubleArray b = DoubleArray.Round(a);

> Output:
[1, 2, 2]

Floor function returns the floor of the elements.

Ceiling function returns the ceiling of the elements.

Reciprocal function returns the reciprocal of the elements in the array.

DoubleArray a = new DoubleArray(new double[] { 2, 4, 5 });
DoubleArray r = DoubleArray.Reciprocal(a);

> Output:
[0.5, 0.25, 0.2]

Unwrap function unwraps a given array by transforming deltas to complement values.

DoubleArray a = new DoubleArray(new double[] { 0, 0.78, 5.55, 7.89 });
DoubleArray u = DoubleArray.Unwrap(a);

> Output:
[0, 0.78, -0.7331853071795864, 1.6068146928204134]

Trunc function return the truncated value of the input.

Sinc function returns the normalized sinc function.

Interpolate function performs linear interpolation over monotonically increasing points.

Statistics

Descriptive Statistics

The Min and Max function returns the minimum and maximum values among the elements of the array. Here's an example of finding the minimum and maximum values in a one-dimensional array:

IntArray a = new IntArray(new int[] { 5, 2, 3 });
double min = a.Min();
double max = a.Max();

> Output:
2
5

In the following example, it returns the minimum and maximum values for each column along the row axis in a two-dimensional array:

IntArray a = new IntArray(new int[,] { { 5, 2, 3 }, { 4, 3, 6 }, { 3, 7, 5 } });
IntArray min = a.Min(Axis.Row);
IntArray max = a.Max(Axis.Row);

> Output:
[3, 2, 3]
[5, 7, 6]

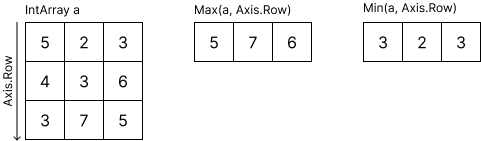
ArgMin and AgrMax methods return the indices of the minimum or maximum values of the array as IntArray.

Additionally, you can use more statistical functions by creating a Stats class.

Below is example that creates a stats class and uses the Mean and Median functions to calculate the mean and median values of an array.

DoubleArray a = new DoubleArray(new double[] { 2, 4, 5, 7, 10 });
Stats stat = new Stats(a);
double mean = stat.Mean();
double median = stat.Median();

> Output:
5.6
5

GeometricMean function returns the geometric mean, and HarmonicMean function returns the harmonic mean.

Variance function returns the sample variance of the elements, and the PVariance function returns the population variance.

DoubleArray a = new DoubleArray(new double[] { 2, 4, 5, 7, 10 });
Stats stat = new Stats(a);
double var = stat.Variance();
double pvar = stat.PVariance();

> Output:
9.3
7.44

Stdev function returns the sample standard deviation of the elements, and the PStdev function returns the population standard deviation.

DoubleArray a = new DoubleArray(new double[] { 2, 4, 5, 7, 10 });
Stats stat = new Stats(a);
double std = stat.Stdev();
double pstd = stat.PStdev();

> Output:
3.0495901363953815
2.727636339397171

Percentile function calculates the percentile of the elements. By providing a value percent between 0 and 100, it returns the percentile of the array elements.

Here's an example of finding the 30th percentile in a one-dimensional array:

DoubleArray a = new DoubleArray(new double[] { 2, 4, 5, 7, 10 });
Stats stat = new Stats(a);
double p = stat.Percentile(30);

> Output:
4.2

Convolution and Correlation

Convolve function returns the linear convolution between two one-dimensional arrays. The default mode is Full, it returns the convolution at each overlapping point. If the mode is Valid, it returns only for points where the signals fully overlap.

DoubleArray a = new DoubleArray(new double[] { 1, 2, 3 });
DoubleArray v = new DoubleArray(new double[] { 2, 3, 4 });
DoubleArray c1 = DoubleArray.Convolve(a, v);
DoubleArray c2 = DoubleArray.Convolve(a, v, ConvolutionMode.Valid);

> Output:
[2, 7, 16, 17, 12]
[16]

Correlate function computes the correlation between two one-dimensional arrays. The dafault mode is Valid.

DoubleArray a = new DoubleArray(new double[] { 1, 2, 3 });
DoubleArray v = new DoubleArray(new double[] { 2, 3, 4 });
DoubleArray c1 = DoubleArray.Correlate(a, v);
DoubleArray c2 = DoubleArray.Correlate(a, v, ConvolutionMode.Full);

> Output:
[20]
[4, 11, 20, 13, 6]

Linear Algebra

The BigParrot Numerics Library provides Linear Algebra functions based on OpenBLAS and LAPACK. The LAPACK library is based on the commercial license of DotNumerics.

Matrix Operations

Inner function computes the inner product of two one-dimensional arrays. It calls the _DOT function from OpenBLAS.

DoubleArray a = new DoubleArray(new double[] { 4, -1, 2 });
DoubleArray b = new DoubleArray(new double[] { 2, -2, -1 });
double c = LinearAlgebra.Inner(a, b);

> Output:
8

Matmul function computes the matrix product of two arrays. For the multiplication between a 2D array and a 1D array, it calls _GEMV from OpenBLAS, and for the multiplication between two 2D arrays, it calls _GEMM.

DoubleArray a = new DoubleArray(new double[,] { { 3, 2 }, { 4, 4 } });
DoubleArray b = new DoubleArray(new double[,] { { 4, 1 }, { 2, 5 } });
DoubleArray c = new DoubleArray(new double[] { 2, 5 });
DoubleArray d = LinearAlgebra.Matmul(a, b);
DoubleArray e = LinearAlgebra.Matmul(a, c);

> Output:
[[16, 13],
[24, 24]]
[16, 28]

Dot function computes the dot product of two arrays. When the arrays are 1-dimensional, it calculates the inner product; when they are 2-dimensional, it performs matrix multiplication.

Outer function computes the outer product of two vectors.

DoubleArray a = new DoubleArray(new double[] { 3, 5, 2, 4 });
DoubleArray b = new DoubleArray(new double[] { 4, 1, 2, 2 });
DoubleArray c = LinearAlgebra.Outer(a, b);

> Output:
[[12, 3, 6, 6],
[20, 5, 10, 10],
[8, 2, 4, 4],
[16, 4, 8, 8]]

Norm function to compute matrix or vector norms. By changing the ord argument you can determine the order of the norm.

DoubleArray a = new DoubleArray(new double[] { 2, 4, 5, 8, 10 });
DoubleArray b = LinearAlgebra.Norm(a);

> Output:
[14.45683229480096]

Matrix Decomposition

QRDecomp function computes the QR decomposition of a matrix. It calls the _GEQRF function from LAPACK.

DoubleArray a = new DoubleArray(new double[,] { { 1, 0 }, { 2, 4 } });
QRReuslt qr = LinearAlgebra.QR(a);

> Output:
Q: [[-0.44721359549995787, -0.8944271909999157],
[-0.8944271909999157, 0.4472135954999581]]
R:[[-2.23606797749979, -3.577708763999663],
[0, 1.7888543819998324]]

Linear Equations

Solve function solves a linear matrix equation or linear scalar equation systems.

Solve the system of equations 1x + 2y = 8 and 3x + 4y = 18:

DoubleArray a = new DoubleArray(new double[,] { { 1, 2 }, { 3, 4 } });
DoubleArray b = new DoubleArray(new double[] { 8, 18 });
DoubleArray s = LinearAlgebra.Solve(a, b);

> Output:
[2, 3]

Lstsq function returns the least-squares solution to a linear matrix equation. It calls the _GELSD function from LAPACK.

DoubleArray a = new DoubleArray(new double[,] { { 0.12, -8.19 }, { 7.69, -2.26 } });
DoubleArray b = new DoubleArray(new double[,] { { 7.30, 0.47 }, { 1.33, 6.58 } });
LstsqResult lstsq = LinearAlgebra.Lstsq(a, b);

> Output:
x: [[-0.08938461072334673, 0.8424188206327871],
[-0.8926405559568749, -0.04504392448401295]]
residuals: []
rank: 2
s: [9.227749561352097, 6.795795614419713]

Eigenvalues

Eigvals function computes the eigenvalues of a general matrix and returns them as a ComplexArray.

DoubleArray a = new DoubleArray(new double[,] { { 2.5, 3.0 }, { -1.5, 2.5 } });
ComplexArray b = LinearAlgebra.Eigvals(a);

> Output:
[2.5+2.1213203435596424j, 2.5-2.1213203435596424j]

Inv function computes the inverse of a matrix.

DoubleArray a = new DoubleArray(new double[,] { { 1.5, 2.5 }, { 3, 3.5 } });
DoubleArray b = LinearAlgebra.Inv(a);

> Output:
[[-1.5555555555555554, 1.111111111111111],
[1.3333333333333333, -0.6666666666666666]]

Polynomial

1-D polynomials

Poly function computes the coefficients of a polynomial with the given specified roots.

DoubleArray a = new DoubleArray(new double[] { 2, -2, 3, -3 });
DoubleArray b = Polynomial.Poly(a);

> Output:
[1, 0, -13, 0, 36]

Roots function returns the roots of a polynomial using the given coefficients.

DoubleArray a = new DoubleArray(new double[] { 3.2, 2, 1 });
ComplexArray b = Polynomial.Roots(a);

> Output:
[-0.3125+0.46351240544347894j, -0.3125-0.46351240544347894j]

PolyInt function returns the integral of the polynomial.

DoubleArray a = new DoubleArray(new double[] { 3, 0, -4, 10, -25 });
DoubleArray b = Polynomial.PolyInt(a);

> Output:
[0.6, 0, -1.3333333333333333, 5, -25, 0]

PolyDer function returns the derivative of the polynomial.

DoubleArray a = new DoubleArray(new double[] { 3, 0, -2, 0, 1, 5 });
DoubleArray b = Polynomial.PolyDer(a);

> Output:
[15, 0, -6, 0, 1]

PolyFit function finds the least squares polynomial fit.

DoubleArray a = new DoubleArray(new double[] { 0, 1, 2, 3, 4, 5 });
DoubleArray b = new DoubleArray(new double[] { 0, 0.8, 1, 0.1, -0.8, -1 });
DoubleArray c = Polynomial.PolyFit(a, b, 2);

> Output:
[-0.16785714285714282, 0.5335714285714283, 0.22142857142857297]

PolyVal function evaluates the polynomial at a specific value.

DoubleArray a = new DoubleArray(new double[] { 3, 2, 1 });
DoubleArray b = new DoubleArray(new double[] { 5, 7, 9 });
DoubleArray c = Polynomial.PolyVal(a, b);

> Output:
[86, 162, 262]

PolyAdd function find the sum of two polynomials.

PolySub function returns subtraction of two polynomials.

PolyMul function find the product of two polynomials.

PolyDiv function returns the quotient and remainder of polynomial division as a tuple.

Signal Processing

The BigParrot Numerics Library provides various signal processing functions for 1-D signals.

The FFT functions of this library is developed based on SharpFFTPack.

https://github.com/dcprojects/SharpFFTPACK

Fourier Transform

FFT function compute the 1-D discrete Fourier Transform.

IFFT function compute the 1-D inverse discrete Fourier Transform.

RFFT function compute the 1-D discrete Fourier Transform for real input.

IRFFT function compute the 1-D inverse discrete Fourier Transform for real input.

double sampleRate = 100;
DoubleArray t = DoubleArray.Linspace(0, 1, (int)sampleRate);
DoubleArray signal = 2 * DoubleArray.Sin(2 * Math.PI * 5.0 * t);
signal += DoubleArray.Sin(2 * Math.PI * 10.0 * t);
ComplexArray rfft = FourierTransform.RFFT(signal);

> Output:
[-1.46549439250521E-14+0j, 0.0158743493535184-0.505129986859598j, 0.0710331473777015-1.12903954639595j, ... ]

FFTFreq and RFFTFreq functions return the discrete fourier transform sample frequencies.

int n = 100;
DoubleArray freq = FourierTransform.FFTFreq(n);

> Output:
[0, 0.01, 0.02, 0.03, 0.04, 0.05, ...]

IIR Filter Design

Butterworth function designs a digital Butterworth filter and returns the filter coefficients as a tuple of the numerator (b) and denominator (a) of the IIR filter. The filter types provided are BandpassFilter, BandstopFilter, LowpassFilter, and HighpassFilter.

The following example designs a Butterworth bandpass filter with a lower cutoff frequency of 0.5 Hz and a higher cutoff frequency of 4.0 Hz. Specify a sample rate of 50 Hz:

double sampleRate = 50;
IIRFilter butter = new IIRFilter(sampleRate);
butter.Butterworth(new BandpassFilter(0.5, 4.0), 2);

> Output:
Numerator: [0.03657483584392803, 0, -0.07314967168785606, 0, 0.03657483584392803]
Denominator: [1, -3.3366117424560837, 4.225986254877656, -2.4258187387209054, 0.537194624801102]

Chebyshev function and the Chebyshev2 function design digital Chebyshev filters and return the filter coefficients as a tuple of the numerator (b) and denominator (a) of the IIR filter.

FIR Filter Design

FirWin function designs an FIR filter using window methods.

double sampleRate = 500;
int numtaps = 51;
DoubleArray f = FilterDesign.FirWin(numtaps, new LowpassFilter(0.5), new HannWindow(), sampleRate);

> Output:
[0, 0.0001571934085247034, 0.0006264885925075509, 0.0014007544233862101, ...]

You can specify the window type in the window parameter. The provided types include the following:

- Hann, Hamming, Cosine, Boxcar, Bohman, Blackman, Blackmanharris, Nuttall, Flattop, Bartlett, Barthann, Kaiser, Gaussian, Tukey

FirWin2 function designs an FIR filter using window methods with the given frequency and gain.

DoubleArray freq = new DoubleArray(new double[] { 0.0, 0.5, 1.0 });
DoubleArray gain = new DoubleArray(new double[] { 1.0, 1.0, 0.0 });
DoubleArray f = FilterDesign.FirWin2(10, freq, gain, new HammingWindow());

> Output:
[0.0006043949948110429, 0.0022830597820518704, -0.01076331842727451, ...]

Filtering functions

LinearFilter function filters IIR or FIR filters along the elements of a 1-dimensional array.

LinearFilterZi function computes the initial conditions zi of the filter delay, which can be added as an argument to the LinearFilter method.

Filtfilt function applies a digital filter to the front and back of a signal.

double sampleRate = 1000;
DoubleArray t = DoubleArray.Linspace(0, 1, (int)sampleRate, false);
DoubleArray signal = DoubleArray.Sin(2 * Math.PI * 10 * t) + DoubleArray.Sin(2 * Math.PI * 100 * t);

IIRFilter butter = new IIRFilter(sampleRate);
butter.Butterworth(new LowpassFilter(50.0), 4);
DoubleArray filtered_signal = SignalTool.FiltFilt(butter.Numerator, butter.Denominator, signal);

> Output:
[0.02570114341383903, 0.08610058414693654, 0.14453572063151063, 0.20100491374962717, ...]

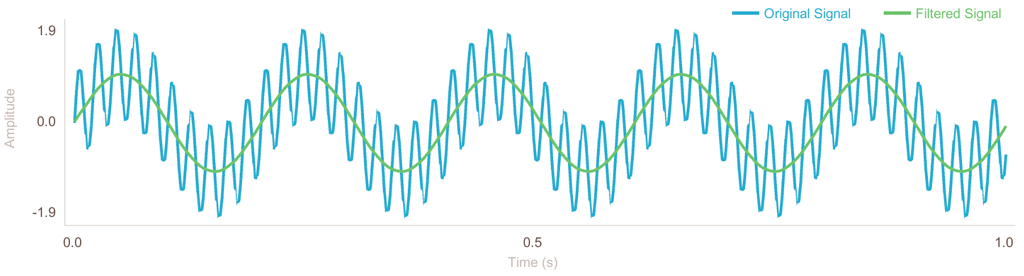
Detrend function removes linear trend from data. You can select detrend type. The Linear type subtracts the result of a linear least squares fit to data. The Constant type only subtracts the mean of the data.

DoubleArray t = DoubleArray.Linspace(0, 5, 100);
DoubleArray x = t + DoubleArray.RandomNormal(new ArrayShape(100));
DoubleArray detrend = SignalTool.Detrend(x);

> Output:
[0.0663569341063954, 0.847824193120883, 0.698679338977181, -1.75450496942743, ...]

Spectral analysis

Welch function estimates the power spectral density using the Welch's method.

double N = 1000;
double fs = 100;
DoubleArray t = 1.0 / fs * DoubleArray.Arange(N);
DoubleArray signal = 0.5 * DoubleArray.Cos(10 * t) + 0.3 * DoubleArray.Sin(30 * t);
Spectrum spec = new Spectrum(signal);
spec.Welch(new HannWindow(), fs);

> Output:
PSD: [0, 0.390625, 0.78125, 1.171875 ...]
Freqs: [0.0001623095656065083, 5.733710576044888E-05, 2.501396467119748E-05, 0.04219553389353737, ...]

The Periodogram function estimates the power spectral density using a periodogram.

Peak finding

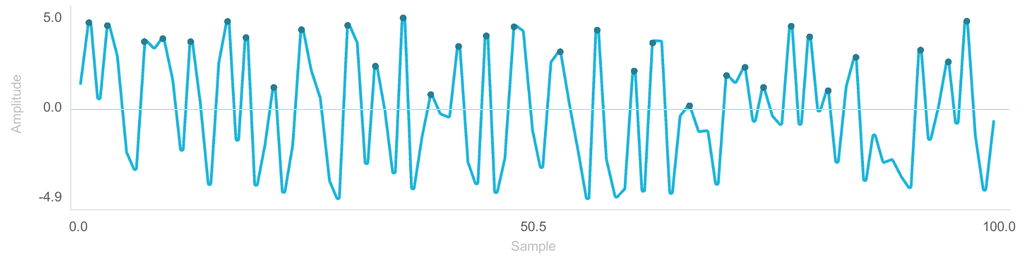
To find peaks within a 1-dimensional array signal, you can create a PeakFinding class and set attributes such as prominence, height, threshold, etc. Then, you can use the Find method to search for peaks. The indices corresponding to the peaks will be stored in the peaks attribute.

DoubleArray signal = DoubleArray.Random(new ArrayShape(100), -5, 5);
PeakFinding peak = new PeakFinding(signal);
peak.heightMin = 0.0;
peak.Find();
IntArray peaks = peak.Peaks;

> Output:
[2, 4, 8, 10, 12, ....]